
(Attractiveness vs. Efficiency)
6 Swimbots
A Swimbot is a two-dimensional object consisting of a set of rectangular parts connected in a tree-like topology. Parts can have varying thicknesses (rectangular heights) and lengths (rectangular widths), as shown in Figure 2.
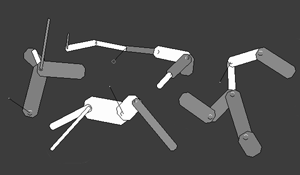
Figure 2. Swimbot anatomies
In this illustration, the ends of the parts are rounded for cosmetics, and bumps are shown to indicate joints. Parts range in length from 5.0 to 20.0, and in thickness from 0.3 to 4.0. Each part has two ends, labeled 0, and 1. Body parts are organized hierarchically, such that each part, as child, has an associated parent part (except for part 0 which has no physical extension but provides the original parent node for all other parts). End 0 of each part is rigidly connected to end 1 of its parent part at a resting angle ranging from -90 to 90 degrees, and is free to rotate about the joint. In the physical model, parts are permitted to intersect other parts (as if they were thin slabs overlapping in the third dimension). Similarly, the model does not recognize collisions between swimbots: they overlap freely with each other as well. Parts come in six colors: red, orange, yellow, green, blue, and violet. Part colors are genetically determined but are not perceivable by other swimbots as a factor in mate choice, and thus are not evolutionarily relevant. They are however useful in visualization, and help in detecting the emergence of distinct local gene pools within the fluid field, since coloration gets reproduced along with other traits.
These various physical attributes among parts do not represent any explicit bodily functions, although the parts of swimmers in evolved populations often exhibit qualitative locomotive or mate-attracting functions.
Part 1 is functionally special in one respect: it possesses the genital and the mouth. The genital is located at end 0, and the mouth is located at end 1. These regions are the foci for mating and eating. They are seen in Figure 2. as short black line segments of length 10, with each segment directed towards the swimbot’s goal. For instance, if a swimbot is interested in food, a segment is seen originating from its mouth and aiming at a food bit, with a dot at the end. If it is interested in mating, a segment is seen originating from the genital and aiming at a potential mate, with a small circle at the end. These graphical elements are used to help visualize the swimbots’ goals and thus to enhance comprehension and intuition while observing the animated simulation.
Motor Control
Swimbots are assumed to have absolute strength to bend parts as their motor control systems dictate, without resistance from friction or torque. They bend their joints in a predetermined, predictable manner, using sine functions as controllers. The angles in the joints of a swimbot change by small increments at each time step. Over extended time, every swimbot part rotates about the end of its parent part in pendulum fashion(back and forth, driven by its associated sine function. Within a single swimbot, all the parts’ sine functions have the same frequency, but overall frequency can vary among different swimbots.
While frequency remains fixed within a single swimbot, amplitudes and phases of these sine functions vary among the parts. The resulting accumulation of this hierarchy of motions (along with variation in anatomy) gives rise to a large variety of complex periodic rhythms, and hence, a large phenotypic space of possible swimming strategies.
The Physics of Swimming
A forward dynamics model is used to generate linear and angular momentum of a swimbot’s body, resulting from body parts moving within a fixed fluid frame, with high viscosity. No fluid dynamics are modeled. Proportional to a friction constant, the motion of each part creates a force in the direction of the normal to the main axis of the part, which is proportional to the sine of the angle between the main axis of the part and the part’s velocity. Part forces are summed to determine the linear and angular forces on the whole body, at each time step of the simulation.
Moving around burns off virtual calories: energy is expended by bending joints and by stroking the fluid. Energy expenditure is proportional to the combined torques required for each joint to rotate the masses of parts on either side, plus friction from parts sweeping through the fluid, times a caloric burn constant.
Energy efficiency in a swimbot is defined to be equal to speed divided by energy expenditure, where speed and energy expenditure are equal to the change in position and energy level, respectively, after each period of 100 time steps.
Mental States
Swimbots have simple brains to accompany their simple goals in life (to eat food and have sex). They do not learn from experience, but just change from state to state, triggered by a few stimuli. The mental states of a swimbot, and their transitions, are borrowed directly from the previous simulation, as shown in Figure 3.
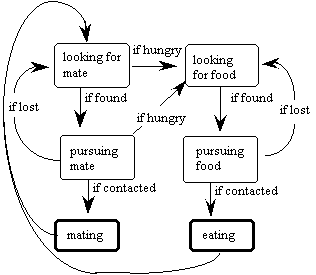
Figure 3. The states of a swimbot and the transitions between them.
All states persist through time until their associated conditions are met, except for the mating and eating states, which are instantaneous. These two states are accomplished when the distance between the swimbot and its goal reaches a distance less than 10.
A looking state transitions to its associated pursuing state when the swimbot has chosen its goal (a food bit or a potential mate). While in a pursuing state, this goal does not change unless a) the swimbot swims away in the wrong direction and loses sight of it, or b) the goal disappears (the food is eaten or the potential mate dies).
Perception
Swimbots can see in all directions(a complete 360 degrees, but cannot see further than a distance of 300 units. Although they are two-dimensional creatures, living in a world analogous to Abbot’s Flatland creatures (Abbott, 63), they can interpret a few properties of the 2D anatomies and motions of companion swimbots as if viewed from outside of the 2D plane. The things a swimbot can perceive are:
1) the direction from its genital to another swimbot’s genital in relation to its own axis of orientation (i.e., the degree it would have to turn in order to orient itself). 2) the direction of a coveted food bit (similar to above) 3) various features of the bodies of other swimbots, such as part sizes, distances between parts, and amounts of movement.
Perceptions 1 and 2 are used to modulate the swimbot’s part amplitudes and phases (as explained in the next section). Perception 3 goes into affect when the swimbot is sizing up potential mates.
Reactivity
This model uses a straightforward stimulus-response mechanism: a swimbot responds to the direction of its current goal (represented by focus vector F in Figure 4) relative to its own orientation (vector O). A swimbot’s orientation is set equal to the main axis of one of its parts (part #1 in the hierarchy). The swimbot’s focus vector continually adapts in order to aim towards its current goal, rotating (as in the hands of a clock) as the relative positions of the swimbot and its goal change.
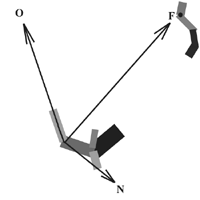
Figure 4. Focus direction compared to orientation
While the actual direction of the goal may sometimes change rapidly in relation to the swimbot’s own orientation (i.e., when the swimbot is near its goal, and both are mobile), its focus direction vector must not change too rapidly since this provides a stimulus which directly modulates the motions of its parts. Thus, to avoid occasional jolts in the body as a result of quick changes in the direction of the goal, a maximum rotation rate is imposed on the focus direction vector so that it cannot rotate more than 1 degree per time step. This lag in adjusting focus is analogous to a lag in visual tracking of a moving target in real animals.
If a swimbot is searching for a mate or food, there is no specific goal and thus no goal direction. In this case, the focus direction vector wanders randomly, rotating by small amounts, as if searching. This behavior enables the swimbot to avoid swimming off in a straight line when there is no specific goal.
The dot product d of the normalized direction vectors O and N (the normal to vector F) is used to modulate the amplitudes and phases of the motions of each body part, so as to affect a turning mechanism. For example, if a swimbot’s goal is to its left, d dictates that it will move its parts in a different rhythm than if its goal is to the right. If vectors O and F are aligned, then d is zero and there is no modulation added to the already existing motions. The amplitude and phase modulators associated with each parts’ motion are genetically-determined (from genes 8 and 9 below). These modulators are multiplied by the dynamically-changing d as the simulation runs, to affect part motions for the sake of turning. The greater d is, the greater the modulation. Since these modulator genes are randomized at initialization, it is up to the forces of evolution to select for a set of modulations which affect better turning to orient towards a goal, as d changes dynamically.
It is interesting to note that, since a swimbot’s overall direction of motion may not necessarily be aligned with its orientation, it does not necessarily have to align vectors O and F in order to move towards its goal.
As noted in the previous simulation, in tracking the overall trajectories of un-evolved swimbots, we get a mixed bag: some spiraling outwards away from the goal, some spiraling in, and many tracing spirals within spirals. These paths, caused by a combination of locomotion style and the stimulus-response mechanism, are reminiscent of the wanderings of Braitenberg creatures [Braitenberg, 84]. Over evolutionary time, these paths become more direct and purposeful.
Genetics
Swimbot genes are represented in fixed-length arrays, consisting of real number values ranging from 0 to 1. In expression from genotype to phenotype, these values are converted into real and integer values, each existing within a pre-determined phenotype-specific range, and used as parameters for building the body and controlling motions. Each swimbot’s genotype consists of 74 values: 2 over-all values (see below), and 72 values controlling 8 possible body parts (with 9 values associated with each of the 8 parts: 9*8=72). Swimbots with fewer than 8 parts still possess latent gene values for a full 8, and continue their reproduction.
The phenotypic effects of each of the genes are:
(for whole swimbot)
1 number of parts (2-8)
2 frequency of motion
(for each possible part)
1 parent part (for connectivity)
2 color
3 resting angle (relative to parent)
4 length
5 thickness
(for sine wave bending)
6 amplitude
7 phase
8 turning amplitude modulator
9 turning phase modulator
Many genetic algorithm techniques have been described in the literature pertaining to the ordering of values within a genotype, and its relation to the problem domain. This model uses a straightforward approach: each set of 9 genes associated with a part are ordered in sequence from 1 to 8. So each part is represented in the genotype by a set of adjacent genes.
Mate Choice
If a swimbot’s energy level is above the hunger threshold (50), and it has not already chosen a mate, it begins looking for one. From the set of potential mates within its circular view horizon, it chooses one whose body provides the most attractive stimuli. The choice is made by ranking the set of potential mate according to one of the following measurements:
Massiveness the sum of all the parts’ sizes
Movement the sum of all the parts’ instantaneous speeds
Openness the sum of all the parts’ distances from the centroid
Length the largest distance between any two parts
When attractiveness is set to equal Massiveness, swimbots choose mates exhibiting comparatively larger bodies than the others within view. When it is set to equal Openness, swimbots choose mates whose parts tend to be splayed outward the most. Attraction to the inverse of these features can also be set. For instance, if attractiveness is set to equal the inverse of Movement, swimbots choose mates who exhibit the least motion.
Reproduction
If swimbots could sing, half the population would be singing the Blues. Mate choice is not necessarily reciprocal in this world: a swimbot’s chosen mate is not guaranteed to have also chosen the chooser, and in fact it is more likely to be concerned with eating a food bit or pursuing its own (possibly indifferent) chosen mate. This simulation does not require mutual consent for reproduction to occur. The inclusion of this requirement was tested briefly, and it was found that the resulting low birth-rate could not sustain the population, given the model settings. While comparing evolutionary dynamics of reproduction with and without mutual consent would be interesting, it is not the central inquiry in this project, and will likely be explored in a subsequent simulation.
When swimbots reproduce, they have exactly one offspring, which is initialized midway between its parents. It inherits a mixture of genes from each parent, using genetic crossover. The offspring genotype is subject to chance mutation (mutation rate = 0.01).
The energy level of each parent is halved during reproduction and the remaining energy is donated to the offspring swimbot. The offspring is born as an "adult" and immediately begins looking for a mate or food. Since parental energy is halved, it sometimes dips below the hunger threshold, and so the parents often begin immediately pursuing food.
Reproduction is rewarded to those swimbots who possess one or more of the following characteristics:
* they are good enough at swimming to reach a desired mate; * they are lucky enough to have found an attractive mate in immediate range (uncommon) * they are attractive enough to have been chosen by a good swimmer as a mate
7 Results
