
(Sexual Swimmers)
7 Running Simulations
7.1 Observations
Swimmers are born hungry (energy at birth is fairly low), and so immediately begin to look for food bits. At initialization, many swimmers are born lucky and happen to be initialized close enough to a food bit that they can eat it immediately. These swimmers then begin looking for mates. Many first generation swimmers are destined to die of hunger, since they do not have enough locomotion skill to reach a chosen food bit. Among those who are able to eat, a small percentage are also able to mate. The result is a high death rate in the first 100,000 time steps or so. Areas in the pond with swimmers whose randomly-initialized genotypes give them a slight advantage will reproduce, thus creating areas of higher birth rate. These areas often blossom into communities, and begin foraging through the fertile Garden of Eden.Figures 3a through 3d show the distribution of swimmers and food at time steps 1, 130,000, 175,000, and 225,000, respectively. 3a and 3b are slightly magnified views of the pond center: 3c and 3d show the entire pond. Food bits can be seen accumulating in the pond, which later become sparse as the swimmer population grows, consuming more food.

Figure 3a. The Garden of Eden - initial distribution
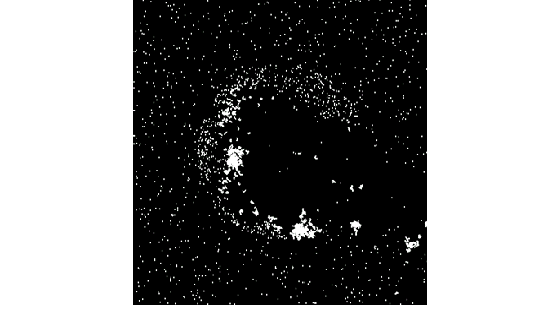
Figure 3b. At 130,000 time steps

Figure 3c. At 175,000 time steps

Figure 3d. At 225,000 time steps
The following sequence of events occurs for most of the simulation runs:
1) A period of occasional random births and deaths, mostly deaths.
2) Among the high death rate, a few pockets of high birth rate appear, indicating presence of successful swimmers.
3) Sudden drop in population count due to first generation swimmers dying of old age (in some simulation runs, the population dies off entirely soon after this point).
4) Increase in population, indicating that some remaining swimmers have inherited locomotion skills and are now reproducing.
5) Groups of genetically related swimmers appearing in isolated areas.
6) Distinct waves of foraging as groups of swimmers move towards areas of high food count, leaving no food in their wake.
7) Population increase in the swimmers, and drop in food count as swimmers mate and eat at higher rate.
8) Consequent drop in swimmer population due to low food supply, with left over swimmers able to eat and mate at a higher rate.
9) Takeover of pond by one or two color groups.
10) After some oscillations, food count vs. swimmer count reach general stability, with occasional new color groups forming and old ones dying off.
11) Increased speed, turning ability, and energy efficiency in swimming usually results over very long periods (in some simulations, the population eventually evolves into graceful one-limbed or two-limbed undulating forms).
Figure 4 shows a typical swimmer vs. food population count for a period of 300,000 time steps. Numbers representing key stages in the above list are annotated at bottom. Maximum swimmer count in this run was 1000. Maximum food count was 3000, indicated by the ceiling at top. The food count is at its maximum value at the start of the simulation, but due to lucky swimmers eating bits in the first time step, the food count appears to begin lower.
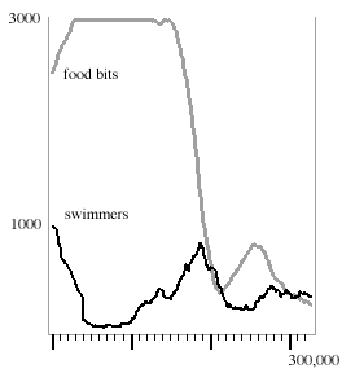
stages... 1 2 3 4 5 6 7 8 9 10 ....11
Figure 4. Swimmer vs. food populations for 300,000 steps
7.2 Turning
As hoped, more optimized locomotion and anatomy emerge in all simulations. Most paths traced by swimmers tend to be spirals of varying types, some paths spiraling out, some in. Some paths create spirals within spirals. The turning mechanism of evolved swimmers tends to correct counterproductive spiraling paths. These stimulus-response behaviors are somewhat reminiscent of the paths exhibited in the classic "Vehicles" of Braitenberg [84]. At the start of a simulation, approximately half of the swimmers (those who can travel at all) spiral away from their chosen mates. Among the others, a few are able to close in on their chosen mates, before getting hungry and sidetracked by a nearby food bit. Indirect paths sometimes resemble mating rituals, and can be amusing to watch - but it only goes this far: these behaviors tend to die out, since more direct paths result in quicker reproduction. The evolution of turning skill involves some quirky behaviors. Some populations acquire the ability to turn in only one direction, and so must do more work in order to orient towards a goal. Some populations have swimmers who actually swim in two modes: backwards and forwards - the two modes being qualitatively different than each other, and one usually being more efficient than the other.7.3 Energy Efficiency
Since energy expended in swimming is proportional to the total magnitude of force a swimmer directs against water, swimmers whose motions are erratic, or whose strokes cancel each other out get hungry often, and so have to spend most of their lives pursing food. They also risk a higher chance of dying of hunger. Thus, they do not mate often, and are likely to die out completely - especially in the presence of more energy-efficient communities in the pond, with their own demands on food. "More efficient swimming" means: 1) closing in on a goal at a higher velocity and 2) expending less energy - than the average swimmer. These terms are not defined numerically in this model, but qualitatively - numerical measurements of swimming efficiency are likely to be made in a subsequent study. The following figures illustrate some of these qualitative observations.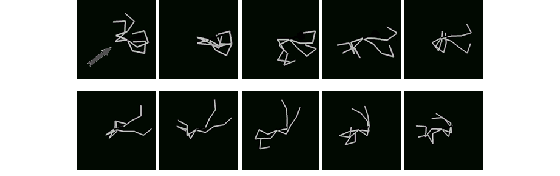
Figure 5. A representative swimmer from a population of 4-limbed, inefficient swimmers.

Figure 6. A representative swimmer from a population of 2-limbed, streamlined, undulating swimmers.
Figure 5 shows a representative swimmer in a color group in the pond comprised of inefficient swimmers, during the earlier stages of a simulation run. Their morphologies include the maximum body-segment count. In this illustration, ten frames from a portion of the characteristic stroke of the swimmer is shown. The swimmer's goal is located at upper right, as indicated by the arrow in the first frame. The two outstretched limbs in frames 6-9 are responsible for most of the locomotive work. The motions of the other two limbs are erratic, probably encumbering.
Figure 6 shows a swimmer with a more streamlined swimming style, exhibited by a color group in the pond contemporary with the group described above (these two communities did not interbreed due to emergent differences in mate preference). In this example, swimming style is graceful and undulating. In the simulation in which the two swimming styles illustrated above were present, the less efficient swimmers were able to sustain their population for more than 100,000 time steps, despite the increasing size of the more efficient group - which eventually took over the pond.
In some rare simulation runs, very aggressive and energy-wasteful swimmers manage to take over the pond. Swimmers of these populations are, consequently, hungry for a larger percentage of their lives, and eat at a high rate, yet are still are able to mate at a sufficient rate to keep the population at a sustainable size. In these populations, food in the pond is sparse, and it is common to see dozens of swimmers racing to try to get to one precious food bit, as shown in Figure 7. In all cases, one swimmer eats the bit, then all the others immediately dissipate to pursue other food bits. In this time-lapse photograph, the direction of the swimmer's goal is shown as a white dash located on its head, oriented at the goal. Multiple animation frames are superimposed in this image to indicate limb movement.

Figure 7. Time-lapse photo of seven aggressive swimmers racing to get to a food bit
Figure 8 shows the characteristic stroke of a swimmer from an advanced population (715,000 time steps). This population has learned to maximize its stroke effect (frame 7), and to avoid drag in follow-through (frames 9, 1).
Two distinct techniques for swimming are noted to emerge: paddling and undulating (and some combinations of both). Figure 5 illustrates paddling behavior, and Figure 6 illustrates a kind of undulating motion. It may have been hubris which originally caused me to anticipate more anthropomorphic limb-stroking techniques to emerge. I was initially disappointed to see many advanced populations reduced to single-limbed undulating eel-like figures (and all that potential anatomy I programmed in was unused!). But in fact, the sea itself illustrates that the most optimized form of underwater travel involves streamlined bodies and sinuous motion.

Figure 8. Nine frames of the stroke cycle of a swimmer from an advanced population
7.4 Results of Sexual Selection
The effects of mate preference are not noticeable in early stages of evolution. Since both body coloration and color preference in mates are initialized randomly, there is no meaningful correlation in these factors at first among swimmers in the population. A swimmer who loves red swimmers may as easily consist of greens and yellows as violets and reds. But small, chance pockets of correlation in these two factors can stimulate higher growth rate in areas of the pond. Eventually, color preferences begin to correlate with actual body colors.It is hypothesized that this happens for two reasons: first, offspring can inherit the colors from the chosen mate along with the preference for that color in the chooser. And at no time can a mating occur when there is NO correlation between a swimmer's color preference and its own body color. Secondly, since this is a spatial model, proto-communities can emerge in local areas of the pond consisting of swimmers who, by virtue of similar preferences - and their proximity - tend to mate within their group only. This inter-group mating then reinforces the group identity further.
It's not possible to show color in these illustrations, but some of the white clumps seen in Figures 3c and 3d are distinctly different in color. In a spatial evolutionary model such as this, the "clumpiness" of phenotype space is often the result of geographic separation, but in this model, differing mate preferences among color groups further encourage phenotypic clumps. This is indicated by the presence of different color groups converging on a common food-rich area but not interbreeding.
To analyze the effects of sexual selection in generating isolated groups, a correlation factor C is defined: a swimmer whose body coloration is homogeneous and whose mate color preference is identical with its body color has a correlation factor of 1. A swimmer whose body coloration has no colors identical to or adjacent to its mate color preference has a correlation factor of 0. All possible phenotypes have correlation factors lying between 0 and 1.
The coherence (propensity for swimmers to go after their own kind) of a group of swimmers is defined by its average correlation factor. That group is also defined as being homogenous in mate preference. Figure 9 shows a plot of correlation factors over the span of 240,000 time steps in a simulation run, with a typical outcome. Every 1000 frames are plotted. It shows correlation factors for each of six groups of swimmers, categorized by the six possible mate color preferences - labeled R, O, Y, G, B and V. Groups comprised of less than 10 swimmers are not plotted. In this plot, R is not shown.
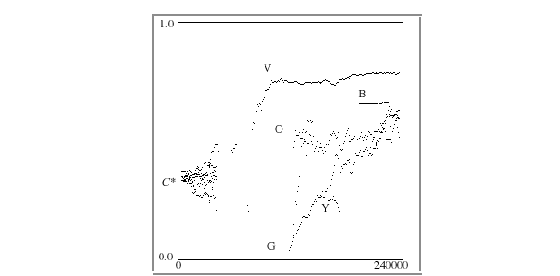
Figure 9. average correlation of mate color preference with swimmer's own body color:
five mate preference groups are plotted over time.
At initialization, correlations are around C* = 0.333 (the theoretical average correlation when genotypes are random - given the model's parameters for color attraction). In this simulation, the whole population size increases around time step 100,000, as the violet group V emerges. This group remains the dominant one throughout the simulation. At one point, a mutation in one area of the pond creates a group of green-loving violet swimmers G. Its average correlation factor is below C*. However, this group persists for many thousands of time steps, and eventually increases the amount of blue in its swimmers' bodies (a color which green-loving swimmers respond to), thus increasing its average correlation factor steadily over time, as shown. Three other groups - O, Y, and B, also emerge, with O persisting.
7.5 Peacock Tail Effect
It appears that sexual selection counteracts a natural selection tendency for streamlined, energy-efficient swimmers with few limbs, due to the fact that swimmers with more limbs can potentially flaunt more colors to admirers. Experiments with simulations run with and without sexual selection support this observation.
8 Future Work
